Aula: Conceitos Fundamentais sobre Pilares

O Papel dos Pilares

Os pilares são elementos estruturais verticais que têm a responsabilidade de transferir as cargas das vigas para as fundações. Eles recebem as cargas provenientes das lajes e coberturas, passando essas cargas para os andares inferiores até chegar às fundações.

Tipos de Seção de Pilares

• Pilares: Elementos com seção retangular ou quadrada.
• Colunas: Elementos com seção circular.

É importante utilizar a nomenclatura correta ao se referir a esses elementos, especialmente em projetos e discussões técnicas.

Esforços nos Pilares

O principal esforço atuante nos pilares é a compressão. No entanto, eles também devem resistir a momentos fletores que podem ocorrer devido a excentricidades na aplicação das cargas.

Dimensionamento de Pilares

Dimensões Mínimas

Segundo a norma, a menor dimensão de um pilar deve ser de pelo menos 19 cm. Em casos especiais, pode-se reduzir para até 12 cm, desde que se aumente o coeficiente de segurança.

Área de Seção Transversal

A área mínima de seção transversal de um pilar deve ser de 360 cm². Isso garante que o pilar tenha capacidade suficiente para resistir às cargas aplicadas.

Índice de Esbeltez

O índice de esbeltez é um parâmetro no dimensionamento de pilares, pois determina a suscetibilidade à flambagem:

• Pilares Curtos: λ ≤ 35
• Pilares Médios: 35 < λ ≤ 90
• Pilares Medianamente Esbeltos: 90 < λ ≤ 140
• Pilares Esbeltos: 140 < λ ≤ 200

Pilares com índice de esbeltez superior a 200 não são permitidos pelas normas devido ao risco elevado de flambagem.

Excentricidades e Segurança

Excentricidade de Primeira Ordem

Causada por deslocamentos iniciais ou por momentos fletores externos, como a ação do vento.

Excentricidade Acidental

Deve-se a imperfeições na execução, como falta de prumo ou retilinearidade, e não está incluída nos coeficientes de ponderação.

Segurança dos Pilares

Aspectos de Segurança

A segurança dos pilares está intimamente ligada às suas dimensões e ao índice de esbeltez. Devemos considerar:

• Robustez: Pilares mais robustos oferecem maior resistência a esforços laterais e flambagem.
• Normas: Seguir as diretrizes normativas, como a NBR 6118, é crucial para garantir que os pilares sejam projetados com segurança.

Comprimento Equivalente

O comprimento equivalente de um pilar é uma medida que ajuda a determinar sua estabilidade. Ele é calculado considerando a distância entre as faces internas das vigas que vinculam o pilar e a altura da seção transversal do pilar.

• Fórmula: O comprimento equivalente é o menor valor entre a distância entre as vigas e a altura do pilar.

Índice de Esbeltez e Classificação

O índice de esbeltez (λ) é calculado usando o comprimento equivalente e o raio de giração. Este índice classifica os pilares em curtos, médios, medianamente esbeltos ou esbeltos, conforme descrito anteriormente. Essa classificação ajuda a determinar o tipo de análise estrutural necessária.

Cálculo do Índice de Esbeltez

• Raio de Giração (i): Calculado pela raiz quadrada do momento de inércia dividido pela área da seção transversal.
• Fórmula do Índice de Esbeltez: \( \lambda = \frac{L_0}{i} \)

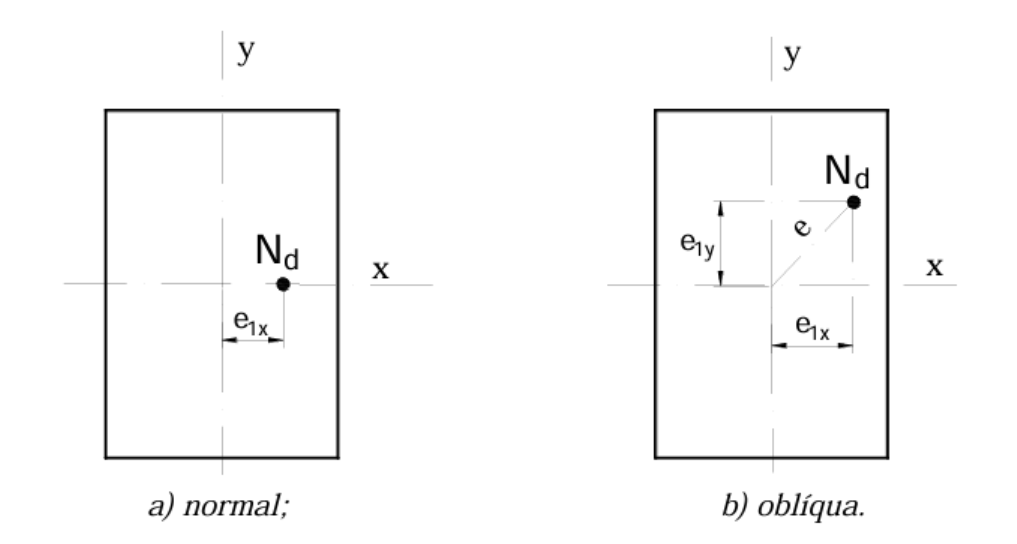
Excentricidades

Excentricidade de Primeira Ordem

A excentricidade de primeira ordem ocorre devido a deslocamentos iniciais na aplicação das cargas. Isso pode ser causado por:

• Deslocamento do ponto de aplicação: A carga não é aplicada exatamente no centro geométrico do pilar.
• Momentos Fletores Externos: Como a ação do vento, que pode gerar um deslocamento adicional.

Excentricidade Acidental

Estas são causadas por imperfeições na execução, como:

• Falta de Prumo: O pilar não está perfeitamente vertical.
• Imperfeições Locais: Deformações ou desvios na forma planejada.

Cálculo das Excentricidades

As excentricidades são levadas em conta no dimensionamento para garantir que o pilar possa resistir aos momentos fletores adicionais gerados por essas condições.

Dimensionamento e Normas

No dimensionamento de pilares, é essencial seguir as normas técnicas para garantir a segurança e a funcionalidade da estrutura. O dimensionamento envolve:

• Verificação de Esmagamento do Concreto: Garantir que o concreto não será esmagado sob carga.
• Cálculo de Armaduras: Determinar a quantidade e a disposição das armaduras para resistir aos esforços de compressão e momentos fletores.

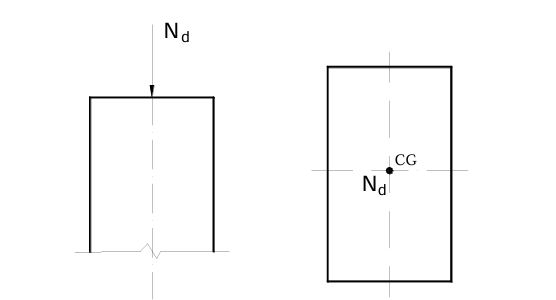
Compressão Simples em Pilares

Definição

A compressão simples em pilares ocorre quando uma força axial é aplicada ao longo do eixo do pilar, resultando em um esforço de compressão uniforme ao longo de sua seção transversal. Esse tipo de esforço é comum em pilares que suportam cargas verticais de lajes e vigas.

Características da Compressão Simples

1. Distribuição Uniforme: A carga é distribuída uniformemente ao longo da seção transversal do pilar, assumindo que a aplicação da carga é centrada e que o pilar é perfeitamente vertical.

2. Esforço Axial: O principal esforço atuante é o axial, que tende a encurtar o pilar.

3. Efeito de P-delta: Em estruturas mais altas ou esbeltas, os efeitos de segunda ordem, como o P-delta, podem influenciar o comportamento do pilar sob compressão.

Cálculo da Compressão Simples

Para calcular a resistência de um pilar sob compressão simples, consideramos a capacidade de carga axial do pilar. Isso é determinado pela fórmula:

\[ N_d = A_c \cdot f_{cd} \]

Onde: - \( N_d \) é a carga axial de cálculo. - \( A_c \) é a área da seção transversal de concreto. - \( f_{cd} \) é a resistência de cálculo do concreto à compressão, dada por \( f_{cd} = \frac{f_{ck}}{\gamma_c} \), onde \( f_{ck} \) é a resistência característica do concreto e \( \gamma_c \) é o coeficiente de ponderação do concreto.

Verificação de Esmagamento

É crucial verificar se a tensão de compressão no concreto não excede a resistência de cálculo do material para evitar o esmagamento. A tensão de compressão é calculada como:

\[ \sigma_c = \frac{N_d}{A_c} \]

Onde: - \( \sigma_c \) é a tensão de compressão no concreto.

Para garantir a segurança, deve-se ter:

\[ \sigma_c \leq f_{cd} \]

Considerações de Projeto

1. Resistência do Material: Escolher um concreto com resistência adequada às cargas previstas.

2. Dimensões do Pilar: Assegurar que as dimensões da seção transversal sejam suficientes para suportar as cargas sem comprometer a estabilidade.

3. Verificação Normativa: Seguir as normas de projeto, como a NBR 6118, para garantir que todos os aspectos de segurança e desempenho sejam atendidos.

---

Compressão Composta em Pilares

Definição

A compressão composta em pilares ocorre quando, além de uma força axial, o pilar também está submetido a um momento fletor. Esse tipo de situação é comum em estruturas onde as cargas não são aplicadas centralmente ou onde há ações laterais, como o vento ou cargas horizontais, que induzem momentos fletores sobre os pilares.

Características da Compressão Composta

1. Esforços Combinados: Na compressão composta, o pilar sofre esforços de compressão axial combinados com momentos fletores. Isso gera uma distribuição de tensões variada ao longo da seção transversal do pilar.

2. Deslocamento Lateral: Momentos fletores podem causar deslocamentos laterais no pilar, aumentando a excentricidade das cargas aplicadas e potencializando efeitos de segunda ordem, como o efeito P-delta.

3. Distribuição Não Uniforme de Tensões: Diferente da compressão simples, onde a distribuição de tensões é uniforme, na compressão composta, as tensões são maiores nas extremidades do pilar, dependendo do sentido e magnitude do momento fletor.

Cálculo da Compressão Composta

O dimensionamento de um pilar sob compressão composta deve considerar tanto a carga axial quanto o momento fletor. A resistência de um pilar nesse estado pode ser calculada considerando a soma das resistências de compressão axial e de momento fletor:

\[ N_d \leq A_c \cdot f_{cd} \quad \text{e} \quad M_d \leq M_{Rd} \]

Onde: - \( N_d \) é a carga axial de cálculo. - \( A_c \) é a área da seção transversal de concreto. - \( f_{cd} \) é a resistência de cálculo do concreto à compressão. - \( M_d \) é o momento fletor de cálculo. - \( M_{Rd} \) é o momento resistente de cálculo da seção transversal do pilar.

Verificação de Segurança para Compressão Composta

Para garantir a segurança do pilar sob compressão composta, devemos verificar se a combinação das tensões de compressão e flexão não excede a resistência do material:

\[ \sigma_c = \frac{N_d}{A_c} + \frac{M_d \cdot y}{I} \]

Onde: - \( \sigma_c \) é a tensão de compressão máxima no concreto. - \( y \) é a distância do centroide até a fibra mais externa da seção. - \( I \) é o momento de inércia da seção transversal.

A verificação de segurança exige que:

\[ \sigma_c \leq f_{cd} \]

Considerações de Projeto para Compressão Composta

1. Dimensionamento Adequado: Garantir que o pilar tenha dimensões adequadas para resistir aos esforços combinados sem comprometer a estabilidade estrutural.

2. Armadura Longitudinal: O uso de armaduras longitudinais é fundamental para resistir aos momentos fletores e assegurar a ductilidade do pilar.

3. Normas Técnicas: Seguir as diretrizes normativas, como a NBR 6118, é essencial para garantir que o pilar sob compressão composta seja projetado de forma segura e eficiente.

4. Efeitos de Segunda Ordem: Considerar os efeitos de segunda ordem em estruturas altas ou esbeltas, onde o efeito P-delta pode influenciar significativamente o comportamento estrutural.

Exemplo de Cálculo

Suponha que um pilar de seção retangular de 30 cm x 40 cm está sujeito a uma carga axial de 500 kN e um momento fletor de 20 kNm. O concreto utilizado tem uma resistência característica \( f_{ck} = 25 \, \text{MPa} \) e um coeficiente de ponderação \( \gamma_c = 1,4 \).

Para garantir que o LaTeX seja interpretado corretamente, é importante formatar as equações com delimitadores específicos para ambientes compatíveis com LaTeX. Aqui está uma versão corrigida com as fórmulas em Markdown que deve funcionar corretamente:

Pilares em Compressão Composta

A compressão composta ocorre quando um pilar é submetido a uma combinação de força axial e momento fletor. Essa combinação exige um dimensionamento cuidadoso para garantir que as tensões resultantes estejam dentro dos limites de segurança.

Parâmetros para Cálculo de Compressão Composta

Vamos considerar um exemplo para ilustrar o cálculo da resistência de um pilar sob compressão composta. Suponha os seguintes dados:

• Dimensões do pilar: 30 cm x 40 cm
• Força axial de cálculo (\(N_d\)): 500 kN
• Momento fletor de cálculo (\(M_d\)): 20 kNm
• Resistência característica do concreto (\(f_{ck}\)): 25 MPa
• Coeficiente de ponderação do concreto (\(\gamma_c\)): 1,4

Ruptura de Pilares